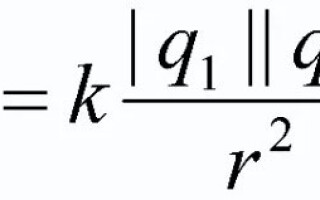Coulombs lov, definisjon og formel - elektriske punktladninger og deres interaksjon

Mellom ladede legemer er det en interaksjonskraft som gjør at de kan tiltrekke seg eller frastøte hverandre. Coulombs lov beskriver denne kraften, viser graden av dens virkning, avhengig av størrelsen og formen på selve kroppen. Denne fysiske loven vil bli diskutert i denne artikkelen.

Coulombs lovformel.

Innhold

1 Stasjonære punktladinger
2 Torsjonsbalanse til Charles Coulomb
3 Proporsjonalitetsfaktor k og elektrisk konstant
4 Retningen til Coulomb-kraften og vektorformen til formelen
5 Hvor Coulombs lov anvendes i praksis
6 Styrkeretning i Coulombs lov
7 Historien om oppdagelsen av loven

Stasjonære punktladinger

Coulombs lov gjelder for stasjonære kropper som er mye mindre enn deres avstand fra andre objekter. En punktelektrisk ladning er konsentrert på slike legemer. Når du løser fysiske problemer, blir dimensjonene til de vurderte kroppene neglisjert, fordi de spiller ingen rolle.

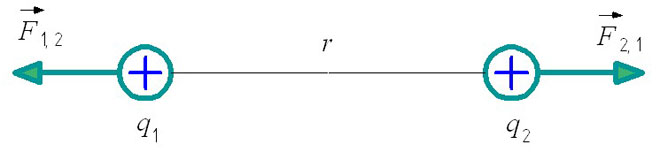
I praksis er punktladninger i hvile avbildet som følger:

Punkt positivt ladet ladning q1.

I dette tilfellet q₁ og q₂ - dette er positivt elektriske ladninger, og Coulomb-kraften virker på dem (ikke vist på figuren). Størrelsen på punktfunksjonene spiller ingen rolle.

Merk! Ladninger i hvile er plassert i en gitt avstand fra hverandre, som i problemer vanligvis betegnes med bokstaven r. Videre i artikkelen vil disse anklagene bli vurdert i et vakuum.

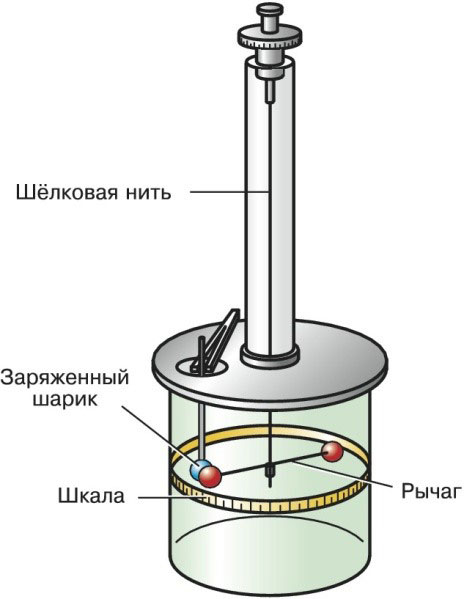
Torsjonsbalanse til Charles Coulomb

Denne enheten, utviklet av Coulomb i 1777, bidro til å utlede avhengigheten til styrken som senere ble oppkalt etter ham. Med dens hjelp studeres samspillet mellom punktladninger, så vel som magnetiske poler.

En torsjonsvekt har en liten silketråd plassert i et vertikalt plan som en balansert spak henger fra. Punktladninger er plassert i endene av spaken.

Under påvirkning av ytre krefter begynner spaken å bevege seg horisontalt. Spaken vil bevege seg i planet til den er balansert av trådens elastiske kraft.

I bevegelsesprosessen avviker spaken fra den vertikale aksen med en viss vinkel. Det tas som d og kalles rotasjonsvinkelen. Når du kjenner verdien av denne parameteren, er det mulig å finne dreiemomentet til de oppkommende kreftene.

Les også: Hva er elektrisk strøm med enkle ord

Torsjonsbalansen til Charles Coulomb ser slik ut:

Torsjonsbalanse til Charles Coulomb.

Proporsjonalitetsfaktor k og elektrisk konstant 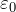$\varepsilon_0$

I formelen til Coulombs lov er det parametere k - proporsjonalitetskoeffisienten eller $\varepsilon_0$ er den elektriske konstanten. Elektrisk konstant $\varepsilon_0$ presentert i mange oppslagsverk, lærebøker, internett, og det trenger ikke å telles! Vakuumproporsjonalitetsfaktor basert på $\varepsilon_0$ kan bli funnet med den velkjente formelen:

$k = \frac {1}{4\cdot \pi\cdot \varepsilon_0}$

Her $\varepsilon_0=8.85\cdot 10^{-12} \frac {C^2}{H\cdot m^2}$ er den elektriske konstanten,

$\pi=3,14$ - Pi,

$k=9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ er proporsjonalitetskoeffisienten i vakuum.

Tilleggsinformasjon! Uten å kjenne til parametrene som er presentert ovenfor, vil det ikke fungere å finne samspillskraften mellom topunkts elektriske ladninger.
Formulering og formel for Coulombs lov

For å oppsummere det ovennevnte, er det nødvendig å gi den offisielle formuleringen av hovedloven for elektrostatikk. Den har formen:

Samhandlingskraften til to punktladninger i hvile i vakuum er direkte proporsjonal med produktet av disse ladningene og omvendt proporsjonal med kvadratet på avstanden mellom dem. Dessuten må produktet av ladninger tas modulo!

$F=k\cdot \frac {|q_1|\cdot |q_2|}{r^2}$

I denne formelen q₁ og q₂er punktavgifter, betraktet som organer; r² - avstanden på planet mellom disse kroppene, tatt på torget; k er proporsjonalitetskoeffisienten ( $9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ for vakuum).

Retningen til Coulomb-kraften og vektorformen til formelen

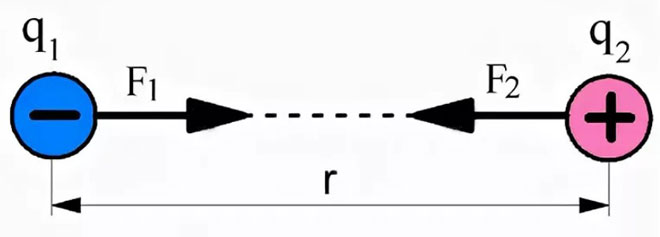
For en fullstendig forståelse av formelen kan Coulombs lov visualiseres:

Retningen til Coulomb-kraften for to punktladninger med samme polaritet.

F_1,2- samhandlingskraften til den første ladningen i forhold til den andre.

F_2,1- samhandlingskraften til den andre ladningen i forhold til den første.

Også når du løser problemer med elektrostatikk, er det nødvendig å ta hensyn til en viktig regel: elektriske ladninger med samme navn frastøter, og motsatte ladninger tiltrekker seg. Plasseringen av interaksjonskreftene i figuren avhenger av dette.

Hvis motsatte ladninger vurderes, vil kreftene til deres interaksjon bli rettet mot hverandre, og viser tiltrekningen deres.

Retning av Coulomb-kraften for to punktladninger med forskjellig polaritet.

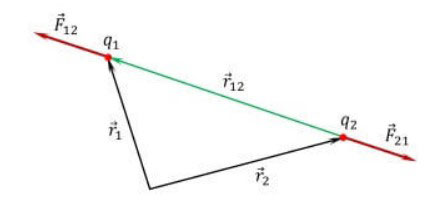
Formelen for den grunnleggende loven om elektrostatikk i vektorform kan representeres som følger:

$\vec F_1_2=\frac {1}{4\cdot \pi\cdot \varepsilon_0}\cdot \frac {q_1\cdot q_2}{r_1_2^3}\cdot \vec r_1_2$

$\vec F_1_2$ er kraften som virker på punktladningen q1, fra siden av ladningen q2,

$\vec r_1_2$ er radiusvektoren som forbinder ladningen q2 med ladningen q1,

Les også: Hvordan lage et elektronisk kretskort hjemme?

$r=|\vec r_1_2|$

Viktig! Etter å ha skrevet formelen i vektorform, må de samvirkende kreftene til topunkts elektriske ladninger projiseres på aksen for å sette tegnene riktig. Denne handlingen er en formalitet og utføres ofte mentalt uten noen notater.

Hvor Coulombs lov anvendes i praksis

Den grunnleggende loven om elektrostatikk er den viktigste oppdagelsen til Charles Coulomb, som har funnet sin anvendelse på mange områder.

Verkene til den berømte fysikeren ble brukt i prosessen med å finne opp forskjellige enheter, enheter, apparater. For eksempel en lynavleder.

Ved hjelp av en lynavleder beskyttes boligbygg og bygninger mot lyn under tordenvær. Dermed økes graden av beskyttelse av elektrisk utstyr.

Lynavlederen fungerer etter følgende prinsipp: under et tordenvær begynner det gradvis å samle seg sterke induksjonsladninger på bakken, som stiger opp og tiltrekkes av skyene. I dette tilfellet dannes et ganske stort elektrisk felt på bakken. I nærheten av lynavlederen blir det elektriske feltet sterkere, på grunn av hvilket en elektrisk koronaladning antennes fra tuppen av enheten.

Videre begynner ladningen som dannes på bakken å bli tiltrukket av ladningen til skyen med motsatt fortegn, slik det burde være i henhold til Charles Coulombs lov. Etter det går luften gjennom ioniseringsprosessen, og den elektriske feltstyrken blir mindre nær enden av lynavlederen. Dermed er risikoen for at lynet trenger inn i bygget minimal.

Merk! Hvis bygningen som lynstangen er installert på, blir truffet, vil det ikke være brann, og all energien vil gå i bakken.

Basert på Coulombs lov ble det utviklet en enhet kalt «Particle Accelerator», som er etterspurt i dag.

I denne enheten skapes et sterkt elektrisk felt, som øker energien til partikler som faller inn i den.

Styrkeretning i Coulombs lov

Som nevnt ovenfor avhenger retningen til de samvirkende kreftene til topunkts elektriske ladninger av deres polaritet. De. Ladninger med samme navn vil frastøte, og ladninger med motsatte ladninger vil tiltrekke seg.

Les også: Hvordan lage en metalldetektor med egne hender, hjelp for nybegynnere

Coulomb-krefter kan også kalles radiusvektoren, fordi de er rettet langs linjen trukket mellom dem.

I noen fysiske problemer gis kropper med kompleks form, som ikke kan tas for en punktelektrisk ladning, dvs. ignorer størrelsen. I denne situasjonen må kroppen som vurderes deles inn i flere små deler og hver del må beregnes separat ved å bruke Coulombs lov.

Kraftvektorene oppnådd ved splitting er oppsummert i henhold til reglene for algebra og geometri. Resultatet er den resulterende kraften, som vil være svaret på dette problemet. Denne løsningsmetoden kalles ofte trekantmetoden.

Retningen til Coulomb-kraftvektorene.

Historien om oppdagelsen av loven

Samspillet mellom to punktanklager av loven vurdert ovenfor ble først bevist i 1785 av Charles Coulomb. Fysikeren klarte å bevise sannheten til den formulerte loven ved å bruke torsjonsbalanser, hvis operasjonsprinsipp også ble presentert i artikkelen.

Coulomb beviste også at det ikke er noen elektrisk ladning inne i en sfærisk kondensator. Så han kom til utsagnet at størrelsen på elektrostatiske krefter kan endres ved å endre avstanden mellom kroppene som vurderes.

Dermed er Coulombs lov fortsatt elektrostatikkens viktigste lov, som mange av de største funnene er gjort på grunnlag av. Innenfor rammen av denne artikkelen ble den offisielle ordlyden av loven presentert, så vel som dens bestanddeler ble beskrevet i detalj.

Lignende artikler: