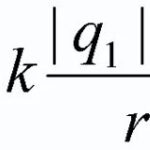Lorentz-styrken og venstrehånden styrer. Bevegelse av ladede partikler i et magnetfelt

Plassert i et magnetfelt dirigentsom gikk gjennom elektrisitet, påvirkes av kraften til Ampere $F_A$ , og verdien kan beregnes ved hjelp av følgende formel:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

hvor $Jeg$ og $l$ - strømstyrke og lederlengde, $B$ - magnetisk feltinduksjon, $\alfa$ - vinkelen mellom retningene til strømstyrken og magnetisk induksjon. Hvorfor skjer dette?

Lorentz kraft. Bevegelse av en ladet partikkel i et magnetfelt.

Innhold

1 Hva er Lorentz-kraften - bestemme når den oppstår, oppnå formelen
2 Bestemme retningen til Lorentz-kraften ved å bruke venstrehåndsregelen
3 Bevegelse av en ladet partikkel i et magnetfelt
4 Anvendelse av Lorentz-styrken i ingeniørfag

Hva er Lorentz-kraften - bestemme når den oppstår, oppnå formelen

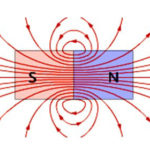
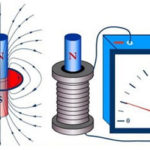
Det er kjent at elektrisk strøm er en ordnet bevegelse av ladede partikler. Det er også fastslått at hver av disse partiklene under bevegelse i et magnetfelt blir utsatt for påvirkning av en kraft. For at en kraft skal oppstå, må partikkelen være i bevegelse.

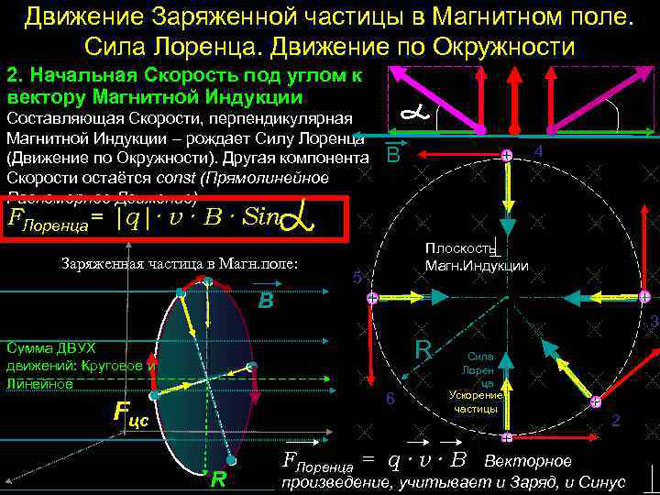
Lorentz-kraften er kraften som virker på en elektrisk ladet partikkel når den beveger seg i et magnetfelt.Retningen er ortogonal til planet der vektorene for partikkelhastighet og magnetisk feltstyrke ligger. Resultatet av Lorentz-styrkene er Ampère-styrken. Når vi vet det, kan vi utlede en formel for Lorentz-kraften.

Tiden det tar for partikkelen å passere gjennom segmentet av lederen, $t = \frac {l}{v}$ , hvor $l$ - lengden på segmentet, $v$ er hastigheten til partikkelen. Den totale ladningen som overføres i løpet av denne tiden gjennom tverrsnittet av lederen, $Q = I\cdot t$ . Vi har her erstattet tidsverdien fra forrige ligning

$Q = \frac {I\cdot l}{v}$ (2)

På samme tid $F_A=F_L\cdot N$ , hvor $N$ er antall partikler i den betraktede lederen. Hvori $N = \frac {Q}{q}$ , hvor $q$ er ladningen til en partikkel. Bytter verdien inn i formelen $Q$ fra (2), kan man få:

$N = \frac {I\cdot l}{v\cdot q}$

På denne måten,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Ved å bruke (1) kan det forrige uttrykket skrives som

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Etter sammentrekninger og overføringer vises en formel for beregning av Lorentz-kraften

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Gitt at formelen er skrevet for kraftmodulen, må den skrives som følger:

Les også: Hvordan konvertere forsterkere til watt og omvendt?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Fordi det $sin\alpha = sin(180^{\circ} - \alpha)$ , så for å beregne Lorentz kraftmodulen spiller det ingen rolle hvor hastigheten er rettet, - i retning av strømstyrken eller mot, - og vi kan si at $\alfa$ er vinkelen som dannes av partikkelhastigheten og magnetiske induksjonsvektorer.

Å skrive en formel i vektorform vil se slik ut:

$\vec{F_L} = q\cdot [\vec{v}\ ganger \vec{B}]$

$[\vec{v}\ ganger \vec{B}]$ er et kryssprodukt, hvis resultat er en vektor med modul lik $v\cdot B\cdot sin\alpha$ .

Basert på formel (3), kan vi konkludere med at Lorentz-kraften er maksimal når det gjelder vinkelrette retninger av den elektriske strømmen og magnetfeltet, det vil si når $\alpha = 90^{\circ}$ , og forsvinner når de er parallelle ( $\alpha = 0^{\sirkel}$ ).

Det må huskes at for å få det riktige kvantitative svaret - for eksempel når du løser problemer - bør man bruke enhetene til SI-systemet, der magnetisk induksjon måles i teslaer (1 T = 1 kg s⁻²·MEN⁻¹), kraft - i Newton (1 N = 1 kg m/s²), strømstyrke - i ampere, ladning i coulombs (1 C = 1 A s), lengde - i meter, hastighet - i m / s.

Bestemme retningen til Lorentz-kraften ved å bruke venstrehåndsregelen

Siden Lorentz-kraften manifesterer seg som Ampère-kraften i makroobjektenes verden, kan venstrehåndsregelen brukes til å bestemme retningen.

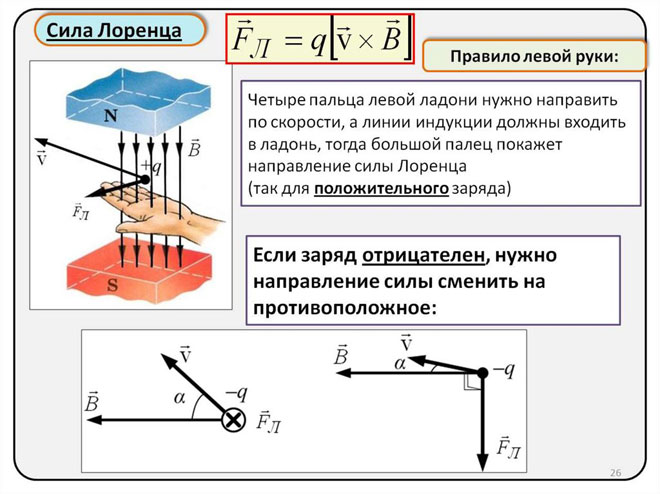
Bestemmelse av virkningsretningen til Lorentz-styrken i henhold til venstrehåndsregelen.

Du må legge venstre hånd slik at den åpne håndflaten er vinkelrett på og mot magnetfeltets linjer, fire fingre skal strekkes i retning av strømstyrken, deretter vil Lorentz-kraften bli rettet dit tommelen peker, som skal bøyes.

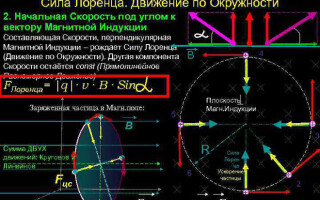
Bevegelse av en ladet partikkel i et magnetfelt

I det enkleste tilfellet, det vil si når vektorene for magnetisk induksjon og partikkelhastighet er ortogonale, kan Lorentz-kraften, som er vinkelrett på hastighetsvektoren, bare endre retning. Størrelsen på hastigheten og energien vil derfor forbli uendret. Dette betyr at Lorentz-kraften virker analogt med sentripetalkraften i mekanikk, og partikkelen beveger seg i en sirkel.

Les også: Hvor mange watt er det i en kilowatt?

I samsvar med Newtons II lov ( $F = m\cdot a$ ) vi kan bestemme rotasjonsradiusen til partikkelen:

$N = \frac {m\cdot v}{q\cdot B}$ .

Det skal bemerkes at med en endring i den spesifikke ladningen til partikkelen ( $\frac {q}{m}$ ) radius endres også.

I dette tilfellet er rotasjonsperioden T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Det er ikke avhengig av hastighet, noe som betyr at den innbyrdes posisjonen til partikler med forskjellige hastigheter vil være uendret.

Bevegelse av en ladet partikkel i et jevnt magnetfelt.

I et mer komplisert tilfelle, når vinkelen mellom partikkelhastigheten og magnetfeltstyrken er vilkårlig, vil den bevege seg langs en spiralformet bane - translasjonsmessig på grunn av hastighetskomponenten rettet parallelt med feltet, og langs sirkelen under påvirkning av dens vinkelrett komponent.

Anvendelse av Lorentz-styrken i ingeniørfag

Kinescope

Kinescope, som sto inntil nylig, da det ble erstattet av en LCD-skjerm (flatskjerm), i hvert TV-apparat, kunne ikke fungere uten Lorentz-styrken. For å danne et fjernsynsraster på skjermen fra en smal strøm av elektroner, brukes avbøyningsspoler, der det dannes et lineært skiftende magnetfelt. De horisontale spolene beveger elektronstrålen fra venstre til høyre og returnerer den tilbake, personellspolene er ansvarlige for den vertikale bevegelsen, og beveger strålen horisontalt fra topp til bunn. Det samme prinsippet brukes i oscilloskoper - enheter som brukes til å studere elektrisk vekselspenning.

massespektrograf

En massespektrograf er en enhet som bruker avhengigheten av rotasjonsradiusen til en ladet partikkel på dens spesifikke ladning. Prinsippet for driften er som følger:

Kilden til ladede partikler, som tar fart ved hjelp av et kunstig skapt elektrisk felt, plasseres i et vakuumkammer for å utelukke påvirkning av luftmolekyler. Partikler flyr ut av kilden og, etter å ha passert langs sirkelbuen, treffer de den fotografiske platen og etterlater spor på den. Avhengig av den spesifikke ladningen, endres radiusen til banen og dermed treffpunktet. Denne radiusen er lett å måle, og når du vet det, kan du beregne massen til partikkelen. Ved hjelp av en massespektrograf ble for eksempel sammensetningen av månejorden studert.

Les også: Hva er yrkene knyttet til elektrisitet

Syklotron

Periodens uavhengighet, og derav rotasjonsfrekvensen til en ladet partikkel fra dens hastighet i nærvær av et magnetisk felt, brukes i en enhet kalt en syklotron og designet for å akselerere partikler til høye hastigheter. En syklotron er to hule metallhalvsylindere - en dee (i form ligner hver av dem den latinske bokstaven D) plassert med rette sider mot hverandre på kort avstand.

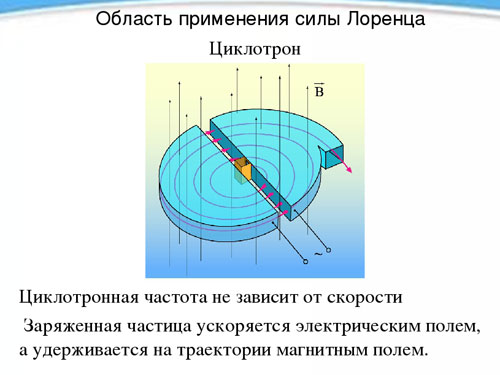
Syklotron - anvendelse av Lorentz-kraften.

Deene plasseres i et konstant ensartet magnetfelt, og det skapes et vekslende elektrisk felt mellom dem, hvis frekvens er lik rotasjonsfrekvensen til partikkelen, bestemt av magnetfeltstyrken og spesifikk ladning. Å bli to ganger i løpet av rotasjonsperioden (under overgangen fra en dee til en annen) under påvirkning av et elektrisk felt, akselererer partikkelen hver gang, øker radiusen til banen, og i et visst øyeblikk, etter å ha oppnådd ønsket hastighet, flyr ut av enheten gjennom hullet. På denne måten kan et proton akselereres til en energi på 20 MeV (megaelektronvolt).

Magnetron

En enhet kalt en magnetron, som er installert i hver mikrobølgeovn, er en annen representant for enheter som bruker Lorentz-styrken. Magnetronen brukes til å lage et kraftig mikrobølgefelt, som varmer opp det indre volumet i ovnen, der maten plasseres. Magnetene som er inkludert i sammensetningen korrigerer banen til elektronenes bevegelse inne i enheten.

Jordens magnetfelt

Og i naturen spiller Lorentz-kraften en ekstremt viktig rolle for menneskeheten. Dens tilstedeværelse lar jordens magnetfelt beskytte mennesker mot den dødelige ioniserende strålingen fra verdensrommet. Feltet tillater ikke ladede partikler å bombardere planetens overflate, noe som tvinger dem til å endre retning.

Lignende artikler: